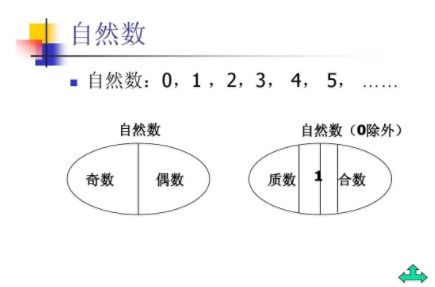
在数学的世界中，有一个基本而重要的概念，那就是自然数。从我们学会数数开始，自然数就伴随着我们的生活，无处不在。那么，自然数究竟如何定义？它具体指代什么？本文将围绕这一主题，对自然数的概念进行深入探讨。

　　自然数，顾名思义，是表示物体个数的数。在数学中，自然数是最基本的数学概念之一，是构建整数、有理数、实数等更复杂数学概念的基础。自然数包括所有的正整数，以及一个特殊的数——0。在数学史上，关于自然数的定义有过多种观点和争论，但现代数学普遍接受的观点是将自然数定义为非负整数。

　　从古至今，自然数的概念一直在不断地演变。在古代，人们用自然数来表示物体个数，例如一只羊、两只狼等。随着数学的发展，人们逐渐发现了自然数的更多性质和规律。在19世纪末，意大利数学家皮亚诺提出了自然数的公理化定义，即皮亚诺公理。这套公理体系以0和后继数为基础，通过五条公理对自然数进行了完整的描述。

　　皮亚诺公理的第一条是：0是自然数。这个看似简单的公理，实际上奠定了自然数的基础。第二条公理是：每个自然数a都有一个后继数a’，且a’也是自然数。后继数的概念相当于在原有自然数的基础上加1。例如，1的后继数是2，2的后继数是3，以此类推。接下来的三条公理分别描述了自然数的相等、不相等和归纳性质。

　　在皮亚诺公理的基础上，我们可以对自然数进行深入的研究。自然数具有以下几个基本性质：

1. 　　唯一性：每个自然数都是唯一的，不存在两个相同的自然数。

2. 　　有序性：自然数之间可以进行比较，且满足大小关系。例如，1小于2，2小于3等。

3. 　　可数性：自然数是可数的，即我们可以通过一个接一个地数数，将所有自然数一一列举出来。

4. 　　运算封闭性：自然数在进行加、减、乘、除等运算时，结果仍然是自然数。

5. 　　归纳性：自然数满足归纳性质，即如果一个性质对自然数1成立，且假设对某个自然数k成立时，也对k的后继数k+1成立，那么这个性质对所有自然数都成立。

　　自然数在数学中具有重要地位，它是数学的基石，也是我们认识和描述世界的基本工具。从简单的计数，到复杂的数学模型，自然数无处不在。此外，自然数在计算机科学、密码学、组合数学等领域也有着广泛的应用。

　　然而，自然数的定义和应用并非一帆风顺。在数学史上，关于自然数的争论和困惑一直存在。例如，0是否应该被视为自然数？有理数和无理数哪个更接近自然数的本质？这些问题引发了无数数学家的思考和探索。

　　总之，自然数是数学中一个基本而重要的概念，它是我们认识世界、解决问题的关键。从皮亚诺公理到自然数的各种性质，自然数揭示了数学的严谨和美妙。随着数学的发展，自然数的概念不断深化，其在各个领域的应用也日益广泛。在未来的数学研究中，自然数将继续发挥其独特的作用，为人类文明的进步贡献力量。

　　在日常生活中，我们常常忽略自然数的重要性。然而，正是这个看似简单的概念，构成了数学的基石，支撑着整个数学体系的建立。从古至今，自然数始终伴随着人类的发展，见证了人类文明的辉煌。正如数学家希尔伯特所说：“数学是自然的皇后，而自然数是数学的皇后。”让我们继续探索自然数的奥秘，感受数学的无穷魅力。